Solving Two-Sum
In Rust of course
The Two Sum problem is a common challenge that you may come across in technical interviews or on coding platforms like LeetCode. Seen as an entry-level question, it's designed to test your understanding of array manipulation and problem-solving.
Imagine you're given an array of numbers, and your task is to identify which two unique elements add up to a given target value. Specifically, you need to return the indices of these numbers.
For instance, let's say your array is `[2, 7, 11, 15]` and the target is 9. The answer would be `[0, 1]` because the numbers at index 0 and index 1 (which are 2 and 7) add up to 9.
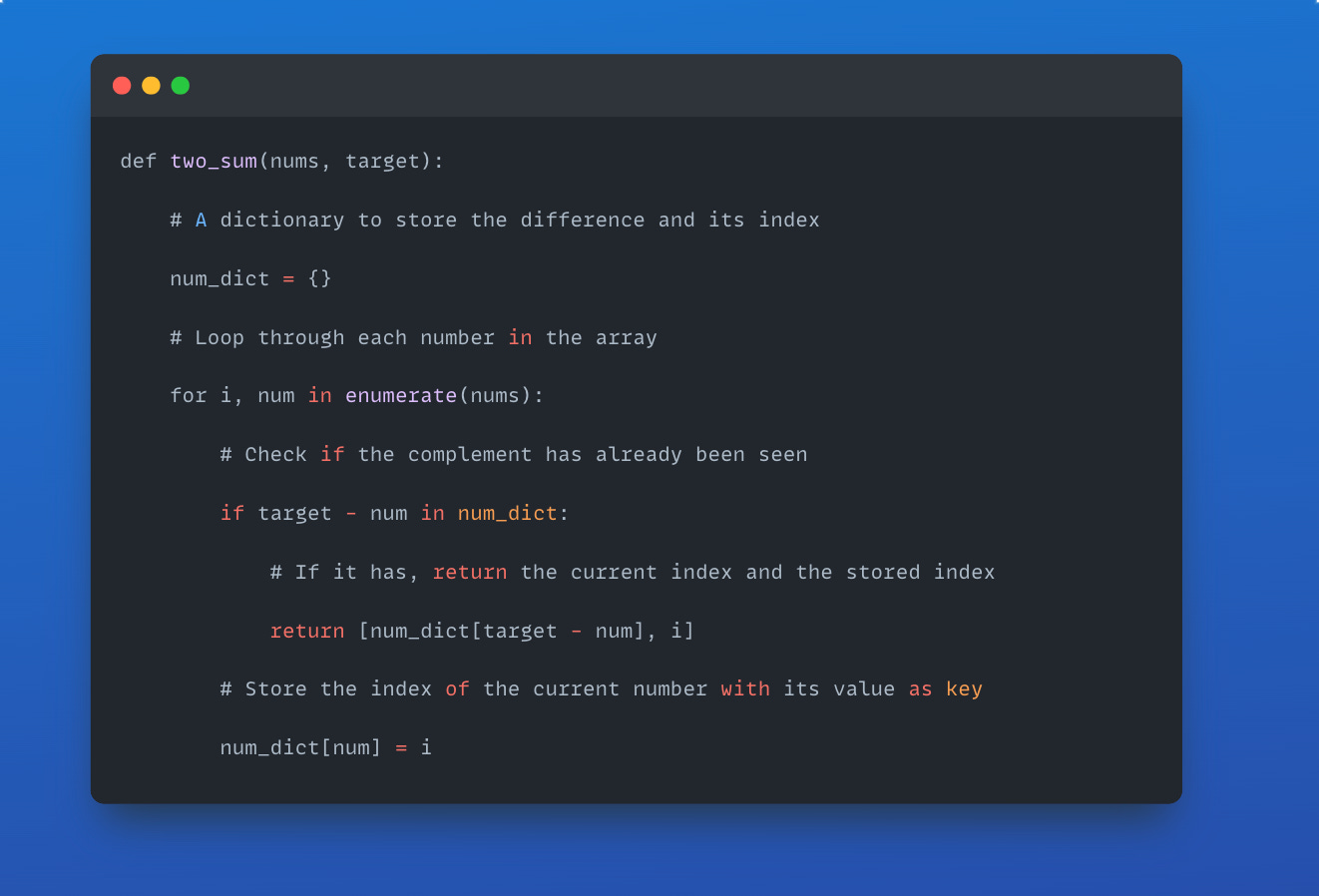
Here's a simple way to solve the Two Sum problem in Python:
To understand how this works, imagine a "complement" – the difference between the target and the current number. You store each number you visit as a key in a dictionary with its index as the value. If you find a number whose complement is already in the dictionary, you have your answer.
Solving Two Sum in Rust
Here's the essence of solving Two Sum in Rust. You'd start by crafting a function that takes in a vector and the target sum. Thanks to Rust's ownership and borrowing rules, when you pass the vector to the function, you ensure safe and efficient memory access.
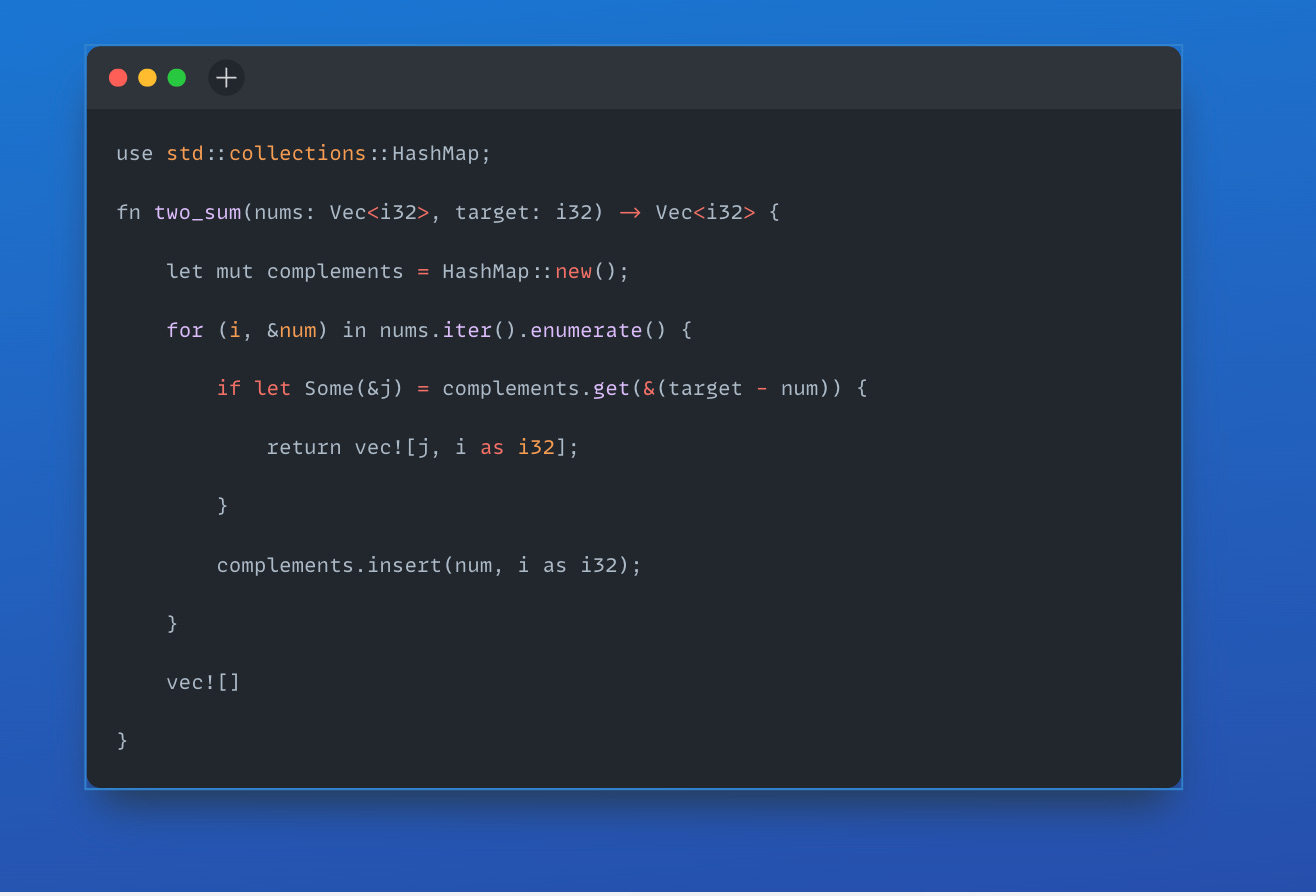
A HashMap is key to an efficient solution. It lets you quickly check if you have already encountered a number's complement – the number needed to reach the target sum when added to the current number. Here's what it might look like in Rust:
In this code, we iterate over the numbers while checking the `complements` HashMap to find a pair that sums to the target. When we find it, we return their indices. If we don't find a pair, we return an empty vector.
Solving Two Sum in Rust can be done in O(n) time complexity, as each element is processed exactly once. Rust's management of memory and performance characteristics shine here, as data is accessed and manipulated efficiently, ensuring that the program's execution is as fast as possible.
In summary, with Rust, you can solve the Two Sum problem effectively, taking advantage of the language's features to ensure both the safety and performance of your solution.
Discussion and Optimization Considerations
In solving the Two Sum problem, trade-offs between different approaches must be weighed. A brute force tactic, which checks every pair to find the sum, is simple but can be slow, with O(n²) time complexity. On the other hand, a more sophisticated method using a HashMap can drop that time complexity to O(n). This is why the HashMap approach is generally chosen—it's swift and efficient, especially when dealing with large datasets.
Rust’s type system plays a significant role when selecting data structures for algorithmic challenges. It promotes robust code by preventing common errors like null pointer dereferencing and buffer overflows. Rust's HashMap, for instance, ensures that key-value operations are fast and safe, crucial for high-performance solutions in the Two Sum problem.
Optimizations to the Rust solution might include using even more performant data structures or tweaking the algorithm to provide early exits once a solution is found to minimize iterations.